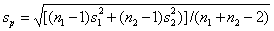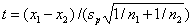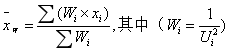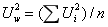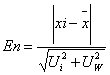实验室间比对是指两个或多个实验室按照预先规定的条件，对相同或类似的测试样品进行检测的活动。它能帮助参与的实验室提高检验质量，建立实验结果的可比性和一致性；为实验室申请认可或资质认定（如CNAS或CMA）提供能力评价的依据。在没有能力验证的领域，实验室可以参加实验室间比对来增强结果的可信性。因此，科学、客观、合理地评价比对结果尤其重要。
实验室根据实际情况组织和符合ISO/IEC 17025能力要求的实验室进行实验室间比对，或者将样品送行业内权威的检测机构检测后进行数据分析。
实验室间比对结果的评定有以下几种统计技术和标准依据：
一、允许误差限判定法
1、方法标准中通常给出了方法再现性限（R)等方法性能指标，依据国家标准（如GB/T 6379），两实验室单一结果的绝对差应满足：
|Lab₁ - Lab₂| ≤ R （其中 R=2.8×再现性标准差）。
2、当方法标准中没有给出再现性等方法性能指标时可以采用不确定度合成的方式：差值需小于两实验室扩展不确定度的合成值：
|Lab₁ - Lab₂| ≤ √(U₁² + U₂²)
3、行业经验值：如色谱分析中，不同实验室平行结果允许差异通常为 ≤平均值的 20%。
二、F检验与t检验法
F检验与t检验通常联合用于两组数据的比较分析，适用于两个实验室间的比对，通过方差分析（F检验）判断两组数据的精密度差异，再通过t检验分析准确度差异。若F值小于临界值表明精密度一致，再结合t值判断均值是否存在显著偏差。具体步骤如下：
1：F检验（方差检验）
目的：判断两组数据的方差是否存在显著差异（精密度是否一致）。
分别计算参加比对的每家实验室多次测试数据的方差σi²
建立假设：
原假设 H₀：σ₁² = σ₂²（方差差异不显著）
备择假设 H₁：σ₁² ≠ σ₂²（方差差异显著）
计算F值：
公式：F = s_max² / s_min²（取较大方差为分子，较小方差为分母）
示例：A实验室方差 sA² = 0.05²，B实验室方差 sB² = 0.022² → F = (0.05)² / (0.022)² ≈ 5.17
确定临界值：
自由度：dfA = nA- 1（大方差组），dfB= nB - 1（小方差组）
查F分布表（α=0.05），或通过软件计算（如Excel：=F.INV.RT(0.05, df1, df2)）
结果判断：
若 F < F表，接受H₀（方差差异不显著）；
若 F > F表，拒绝H₀（方差差异显著）
2：t检验（均值差异检验）
前提：F检验通过（方差差异不显著）
目的：判断两组数据的均值是否存在显著差异。
建立假设：
H₀：μ₁ = μ₂（均值无差异）
H₁：μ₁ ≠ μ₂（均值有差异）
计算t值：
合并标准差：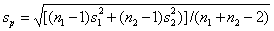
t值公式：
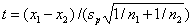确定临界值：
自由度 df = n₁ + n₂ - 2
查t分布表（α=0.05，双侧检验）
结果判断：
若 |t| < t表，接受H₀（均值无显著差异）；
若 |t| > t表，拒绝H₀（均值有显著差异）
关键总结：
F检验不通过：说明两组数据方差差异大，需用校正t检验（如Welch's t检验）；
顺序不可逆：先F检验，后t检验。
当参加比对的实验室超过2家时，也可以将各家实验室的方差按从小到大的顺序排列，用F检验检验这组方差中的最大方差与最小方差。如果两者没有显著性差异，则介于这两者之间的方差也可以认为没有显著性差异。如果最大的和最小的方差差异显著，则需要再进行两两比较或按照其他方式来处理（此处不展开）。
三、En比较法
各实验室不确定度已知，当各实验室不确定度没有明显差异时，可以将各实验室测试结果的算术平均值作为平均值；当各实验室不确定度有明显差异时，按下式计算结果的加权平均值和整体标准不确定度：
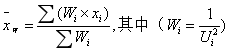
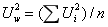
En值按下式计算：
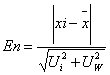当En小于等于1时，结果满意，当En大于1时，结果不满意。
四、Z值比较法
Z值比较法是能力验证时常用的方法，适用于参加比对的实验室数量较多的情况，通过实验室与中位值的偏差相当于多少倍标准化IQR（四分位距）来评估实验室结果的一致性。此处不再展开。
关键步骤总结：
1、明确检测项目对应的标准的方法特性，用允许误差（如再现性限等）判定；
2、没有方法特性参数时：两家选择F/t检验，多实验室时采用En值或Z值比较。
